이산수학 2. 명제 논리의 응용, 동치(equivalence)와 만족가능성(satisfiability)

안녕하세요 블레이즈 입니다. 

 

지난 포스팅에서 명제 논리를 공부했습니다. 

 

이번 포스팅에서는 명제 논리의 좀 더 심화 개념을 알아보도록 하겠습니다. 

 

먼저 첫 번째 문제는 

You can graduate only if you have completed the requirements of your major and you do not owe money to the university and you do not have an overdue library book.

라는 문장이 있을 때 이 문제를 명제와 기호로 표현해보는 것입니다. 

 

 

g를 “You can graduate,” 

m을 “You owe money to the university,” 

r을 “You have com- pleted the requirements of your major,”

 b를 “You have an overdue library book.” 라고 하면 다음과 같이 정리할 수 있습니다. 

 

 

 

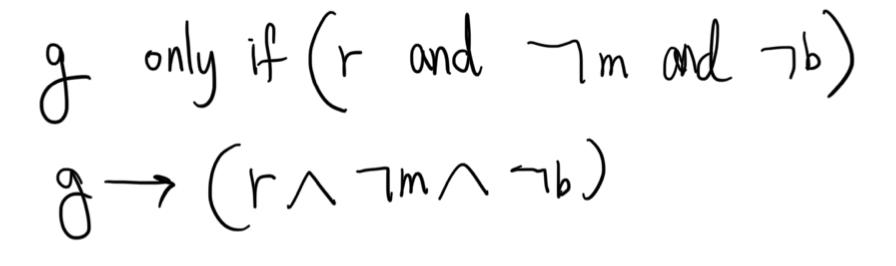
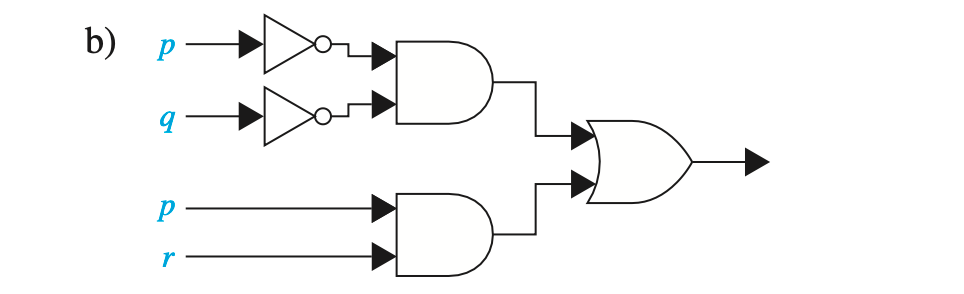
두 번째 문제는 아래의 복합 회로를 명제 논리로 나타내는 것입니다. 

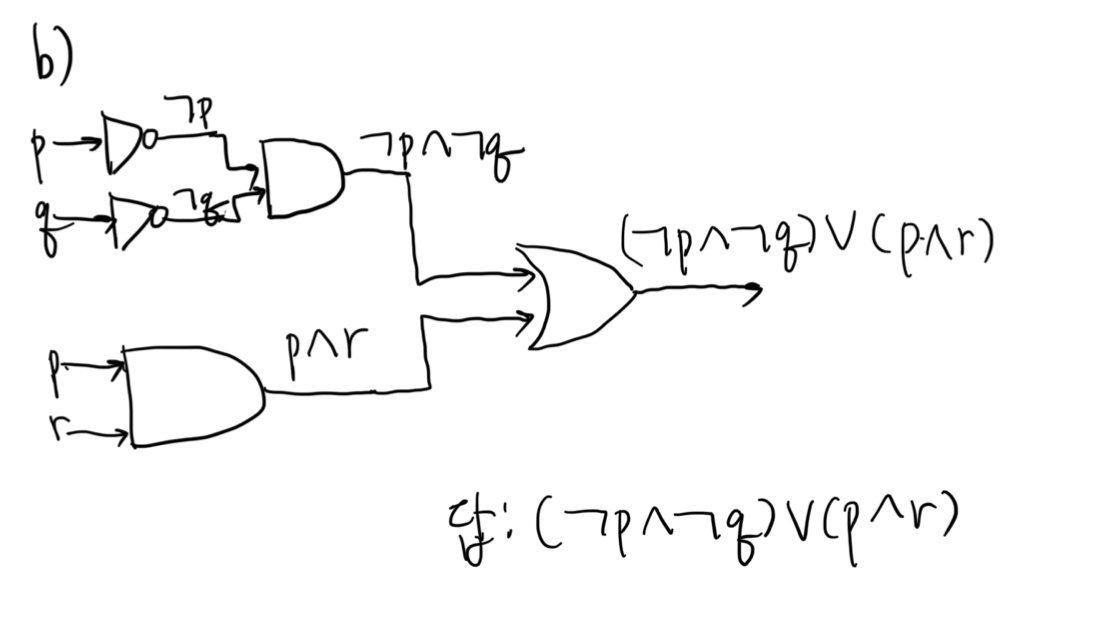
위의 이미지처럼 화살표를 따라가면서 기호로 표시하면서 풀었더니 

그렇게 어렵지 않더라고요!

 

 

 

세 번째 문제는 p↔q와 (p→q)∧(q→p) 가 논리적으로 동치임을 증명하는 문제입니다. 

 

저는 진리표를 만들어서 모든 경우에서 각각의 명제 논리의 진리값이 동일함으로 보여서 증명을 했습니다. 

 

 

네 번째 문제는 복합 명제를 만들어내는 문제입니다. 

구체적으로는 p, q, r을 포함하고 있는데 p와 q가 참이고 r이 r이 거짓일 때만 참이고

그 외의 경우엔 모두 거짓인 복합명제를 만들라는 문제입니다. 

 

[Hint: Use a conjunction of each propositional variable or its negation.]