이산수학 9. 정렬성 원리(well ordering property), 재귀함수(Recursive functions)

안녕하세요 블레이즈입니다. 

이번 포스팅에서는 정렬성 원리와 재귀적으로 정의된 함수에 대해서 알아보도록 하겠습니다. 

 

 

첫 번째 문제는 모든 양의 정수 k와 n에 대하여 아래의 식이 성립함을 보이는 것입니다.

저는 정렬성 원리(well ordering property)를 사용해보겠습니다. 

 

 

두 번째 문제입니다. 이 문제는 비트 문자열을 재귀적으로 정의해보는 문제입니다. 

 

1보다 0이 많은 비트 문자열을 재귀적으로 정의하기.

 

 

세 번째 문제입니다. 이 문제는 재귀적으로 정의된 함수에 대해서 일반항을 구해야 하네요. 

f (n) 은 다음을 만족한다. 

 f(n) < f(m) when n < m

 

f(k)가 다음과 같이 재귀적으로 정의되어 있다.

 

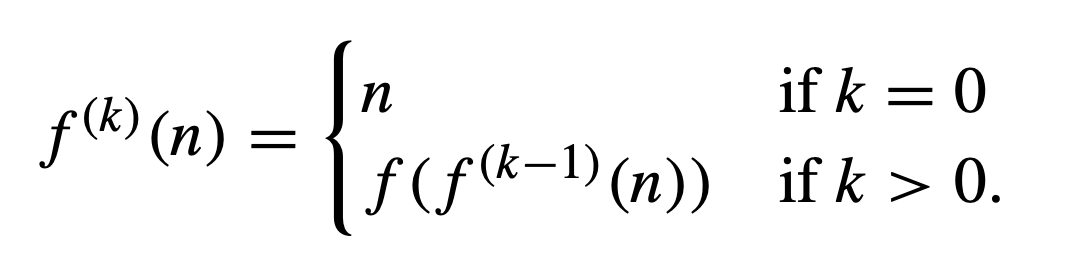
 c가 양의 실수일 때,   f c∗ 는 그 값이 c 이하가 되기 위해 반복되어야 하는 f의 반복횟수 이다.

다시 말해  fc∗(n) 는 음이 아닌 정수 중 가장 작은 값이며 다음을 만족한다. fk(n)≤c.