안녕하세요 블레이즈 입니다.

이번 포스팅에서는 이산수학에서 사용하는 함수의 정의와 활용에 대해서 공부해보겠습니다.
첫 번째 문제입니다. 이 문제는 함수가 실수에서 실수로 정의된 전단사 함수(bijection)임을 확인하는 문제입니다.
a) f(x)=−3x+4
b)f(x)=−3x2+7
c) f(x)=(x+1)/(x+2)
d) f(x)=x5+1

정의역에서 문제가 없고 순수하게 증가만 하는 함수는 bijection임이 당연해서 특별히 증명은 하지 않았습니다.
두 번째 문제입니다. 두 번째 문제는 첫 해 연봉이 5만 달러인 직원의 차후 연봉에 대해 예상해보는 문제입니다. 점화식(recurrence relation)으로 연봉을 나타내보라는 것 같네요.
"한 직원이 2009년에 연봉 5만 달러로 입사했다.
매년 연봉인상이 이뤄지는데 지난 해 연봉의 5%와 1000달러가 오른다."
저는 먼저 Sn을 정의를 내리고 시작했더니 조금 편했던 것 같습니다.
a) 2009년 이후로 n 년이 지났을 때의 연봉을 점화식으로 나타내기.


b) 2017년의 연봉은?

c) 2009년 이후로 n 년이 지났을 때의 연봉을 일반식으로 나타내기.

세 번째 문제입니다. 이 문제는 수열의 합 공식을 유도하는 문제입니다. 고등학교 교과과정에서 배우는 내용인데 직접 증명을 다뤄봤습니다.
다음의 식에 대한 공식을 유도하기.
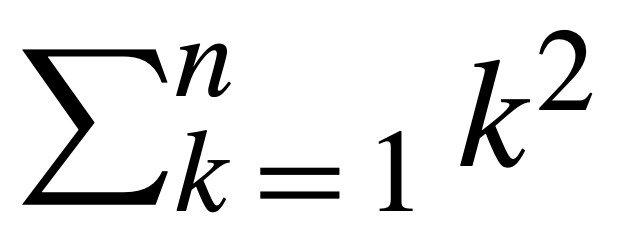
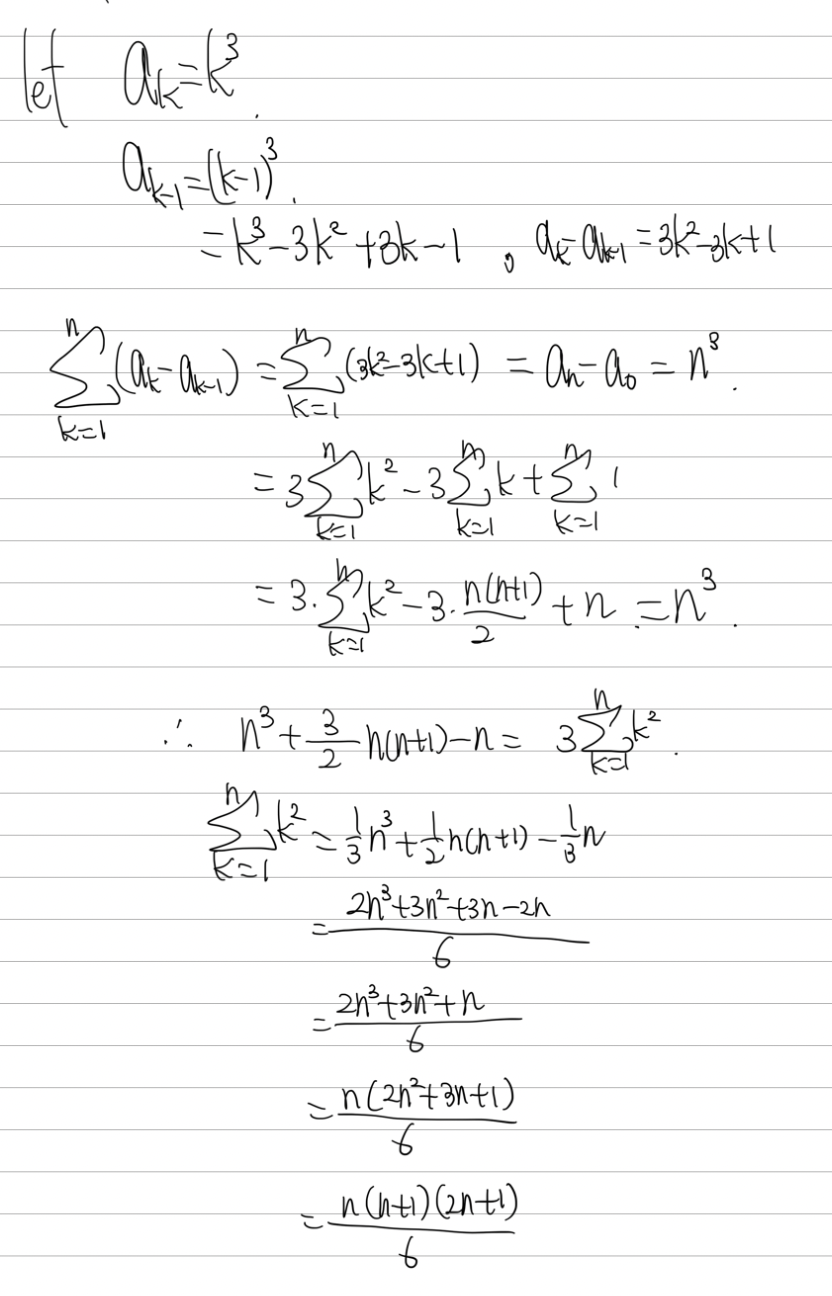
감사합니다.
블레이즈 테크 노트
Blaze Tech Note
'이산수학(Discrete Math)' 카테고리의 다른 글
| 이산수학 8. 시간 복잡도, 계산 복잡도, 알고리즘 복잡도(Time Complexity, Complexity of Algorithms) (0) | 2023.07.08 |
|---|---|
| 이산수학 7. 행렬 매트릭스 (0) | 2023.07.07 |
| 이산수학 5. 명제논리 이산수학의 증명 문제(Proof Methods and Strategy) (0) | 2023.07.05 |
| 이산수학 4. 명제논리 중첩된 한정기호(Nested Quantifiers)와 추론 규칙(Rules of Inference) (0) | 2023.07.04 |
| 이산수학 3. 명제논리 술어(Predicates)와 한정 기호(Quantifiers) (0) | 2023.07.03 |




