안녕하세요
블레이즈입니다.

오늘은 이산 수학에서 자주 볼 수 있는
간단한 증명 문제 풀이를 해보고자 합니다.
증명에서 사용할 수 있는 전략이 몇 가지 있는데 이번 포스팅은 이 증명 전략을 활용해볼 것입니다.
첫 번째 문제입니다. 첫 번째 문제는 가정을 통해 원하는 결과를 도출해내는 전략입니다.
if x is rational and x ≠ 0, then 1/x is rational 임을 증명하기

QED는 증명 완료라는 의미입니다.
두 번째 문제입니다. 두 번째 문제는 반례를 제시해서 주어진 statement가 거짓임을 보이는 전략입니다.
다음의 문장이 거짓임을 증명하기.
Every positive integer can be written as the sum of the squares of three integers.


세 번째 문제입니다. 세 번째 문제는 가능한 모든 경우를 나눈 다음, 각 경우에서 모두 성립함을 보이는 전략입니다.
다음의 문장이 참임을 증명하기
If x and y are real numbers, then max(x, y) + min(x, y) = x + y.
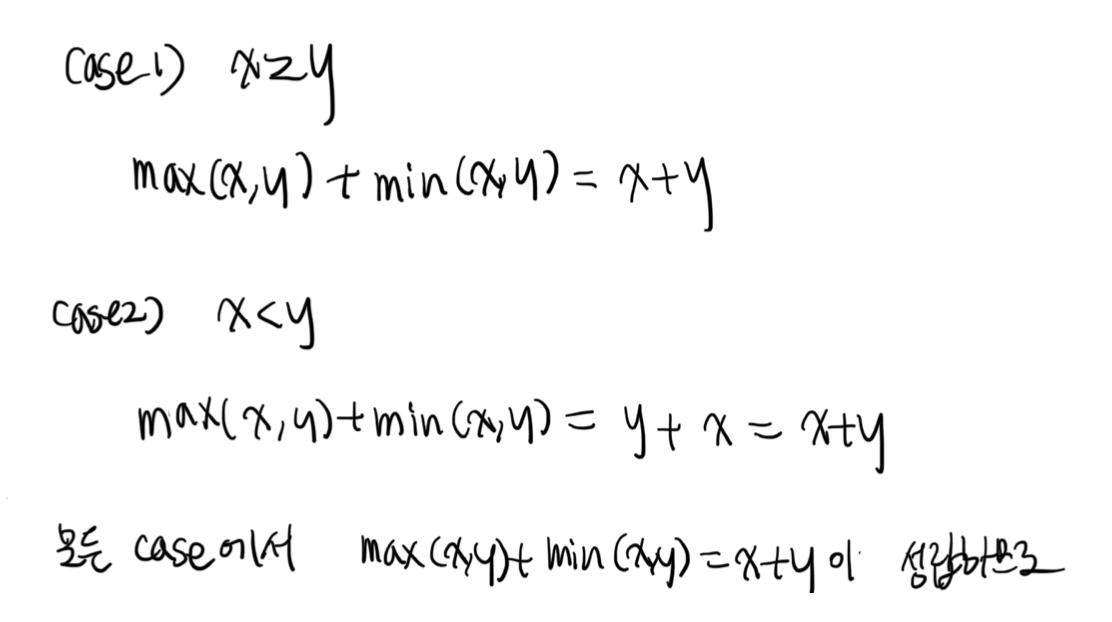

네 번째 문제입니다. 네 번째 문제 역시 경우를 나눠서 증명하는 풀이입니다.
경우를 나누면 문제가 간단해져서 풀이가 쉬워질 수 있습니다.
min(a, min(b, c)) = min(min(a, b), c) whenever a, b, and c are real numbers 이 참임을 보이기.


감사합니다.
블레이즈 테크 노트
Blaze Tech Note
'이산수학(Discrete Math)' 카테고리의 다른 글
| 이산수학 7. 행렬 매트릭스 (0) | 2023.07.07 |
|---|---|
| 이산수학 6. 함수 전단사, 점화식, 수열과 수열의 합 (0) | 2023.07.06 |
| 이산수학 4. 명제논리 중첩된 한정기호(Nested Quantifiers)와 추론 규칙(Rules of Inference) (0) | 2023.07.04 |
| 이산수학 3. 명제논리 술어(Predicates)와 한정 기호(Quantifiers) (0) | 2023.07.03 |
| 이산수학 2. 명제 논리의 응용, 동치(equivalence)와 만족가능성(satisfiability) (0) | 2023.07.02 |




