안녕하세요
블레이즈 테크노트의
블레이즈입니다.

오늘은 이항정리에 대해서 공부해보려고 합니다.
이항정리는 어떻게 보면 제곱식의 전개를 예측할 수 있는 정리입니다.
이 이항정리를 증명해보는 것이 오늘의 문제입니다.
저는 수학적 귀납법을 이용해 증명했습니다.


다음은 조합에 대한 다양한 문제 상황에 대한 문제입니다.
5개의 공을 3개의 박스에 나누는 방법이 몇가지인지 구하시오. 단, 모든 박스는 최소 1개의 공을 담고 있어야 한다.
a) 공과 상자에 모두 이름표가 있을 때
b) 공은 이름표가 있지만 상자는 구분할 수 없을 때
c) 공은 구분할 수 없고 상자는 이름표가 있을 때
d) 공과 상자 모두 구분할 수 없을 때


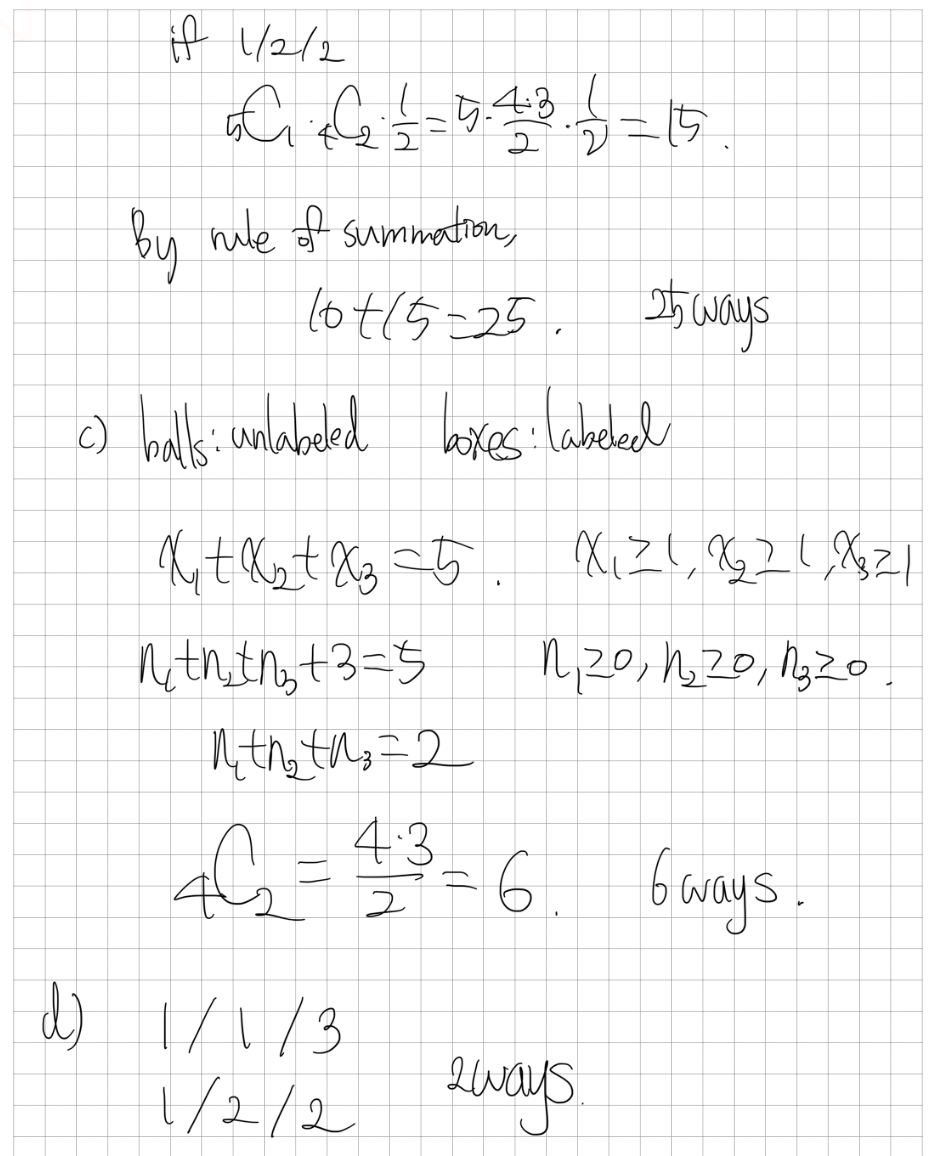
감사합니다.
블레이즈 테크노트
'이산수학(Discrete Math)' 카테고리의 다른 글
| 이산수학 14. 평균과 분산 공식 증명과 점화식 (0) | 2023.07.23 |
|---|---|
| 이산수학 13. 확률계산을 위한 기초, 조건부 확률 (0) | 2023.07.22 |
| 이산수학 11. 조합적 증명과 개수 세기(Counting) (0) | 2023.07.11 |
| 이산수학 10. 재귀 알고리즘과 개수 세기(Counting) (0) | 2023.07.10 |
| 이산수학 9. 정렬성 원리(well ordering property), 재귀함수(Recursive functions) (0) | 2023.07.09 |




