안녕하세요 블레이즈입니다.

이산수학은 컴퓨터 프로그래밍 과정에서 기초가 되는 학문입니다.
명제 논리는 p이면 q이다 와 같은 문장을 뜻하는데요
이러한 논리 관계를 잘 알면 아무래도 좋을 것입니다.
문제와 함께 알아보도록 하겠습니다.
첫 번째 문제는 해당 영어 문장이 inclusive or 인지, exclusive or 인지 판별하고 그 이유를 설명하는 문제입니다.

두 번째 문제는 조건문(conditional statement)에 대하여 역(converse)과 대우(contrapositive), 이(inverser)를 적어보는 문제입니다.
a) If it snows today, I will ski tomorrow.
b) I come to class whenever there is going to be a quiz.
c) A positive integer is a prime only if it has no divisors other than 1 and itself.


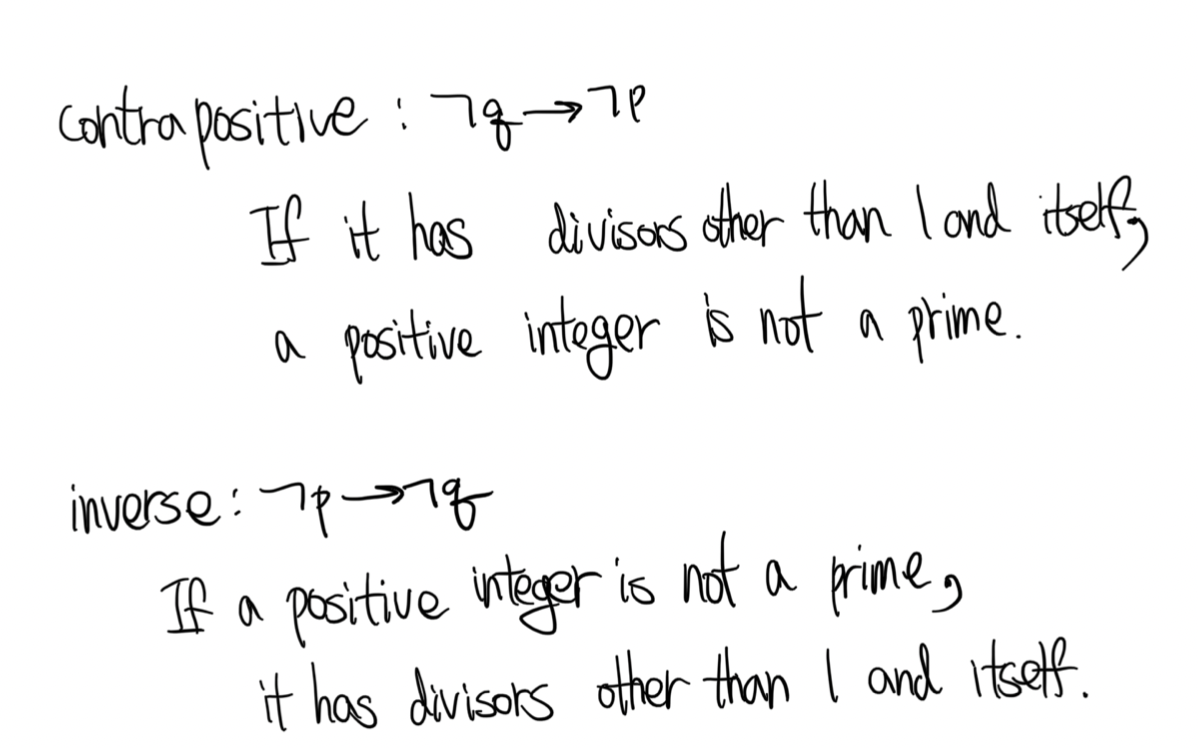
세 번째 문제는 아래의 복합 명제에 대하여 진리표를 만들어보는 것입니다.
make truth table
a) p→¬p
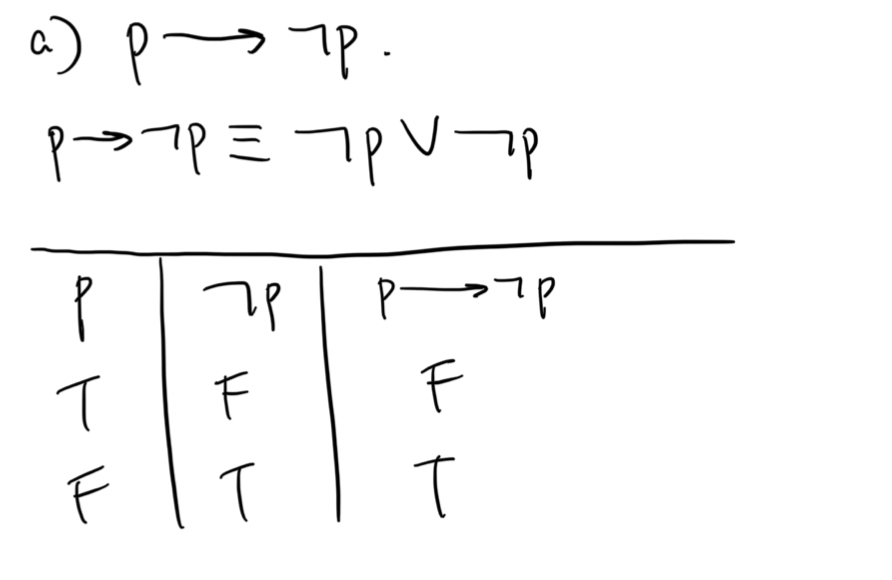
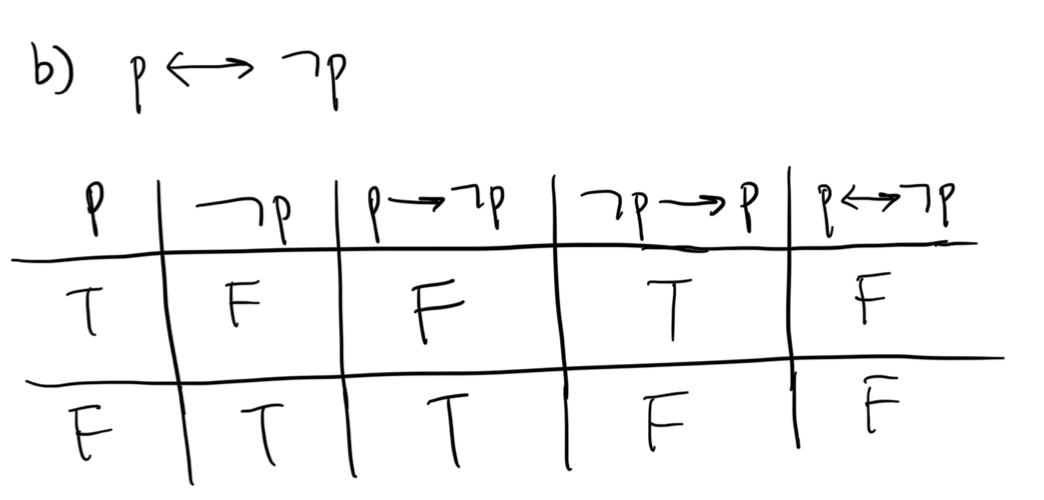
b) p↔¬p
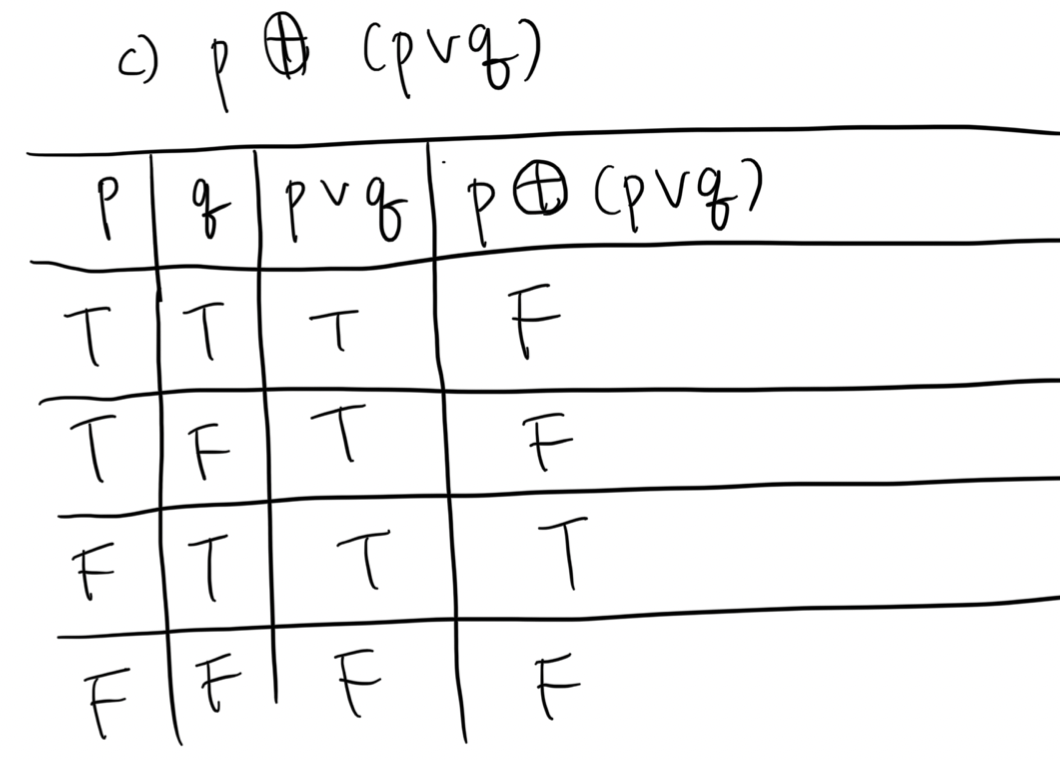
c) p⊕(p∨q)
d) (p∧q)→(p∨q)
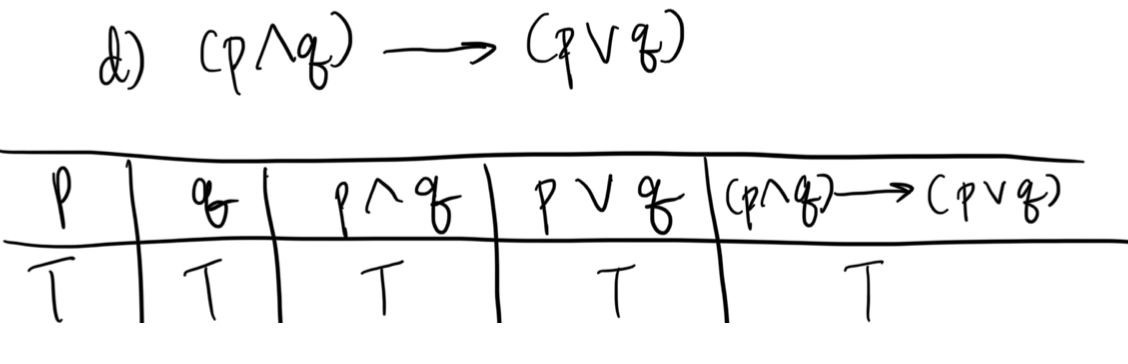
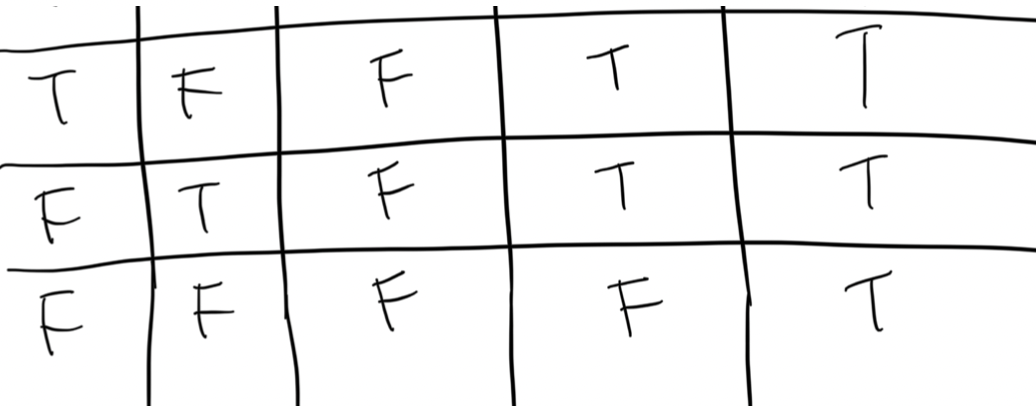
e) (q→¬p)↔(p↔q)

f) (p↔q)⊕(p↔¬q)


'이산수학(Discrete Math)' 카테고리의 다른 글
| 이산수학 6. 함수 전단사, 점화식, 수열과 수열의 합 (0) | 2023.07.06 |
|---|---|
| 이산수학 5. 명제논리 이산수학의 증명 문제(Proof Methods and Strategy) (0) | 2023.07.05 |
| 이산수학 4. 명제논리 중첩된 한정기호(Nested Quantifiers)와 추론 규칙(Rules of Inference) (0) | 2023.07.04 |
| 이산수학 3. 명제논리 술어(Predicates)와 한정 기호(Quantifiers) (0) | 2023.07.03 |
| 이산수학 2. 명제 논리의 응용, 동치(equivalence)와 만족가능성(satisfiability) (0) | 2023.07.02 |




